Lab 3

Lab 3: Non-Constant Acceleration Activity

Lab Members:

Jarrod Griffin

Christina Vides

Enio Rodriquez

In this activity, we work on a problem by hand, and then by using Microsoft Excel. 

Introduction: For this lab, we found an answer for the rocket elephant problem in two different ways, and then compared the accuracy of the answers, and how we could make the answer provided by Excel more accurate.

Apparatus/Procedure: The only material required for this lab was a laptop with Microsoft Excel. We initially worked through the problem, which involved finding how far an elephant would go before stopping, using an analytical approach, and then by using Excel to calculate an answer. When doing the calculations by hand, it required the use of calculus, and hoping that we got an integral that would properly integrate. We followed the procedure of working out the problem by hand that was defined in our lab book. All calculations were already worked out for us in the lab manual. The way Excel was to be set up was also described in detail in the manual.

Excel Data:

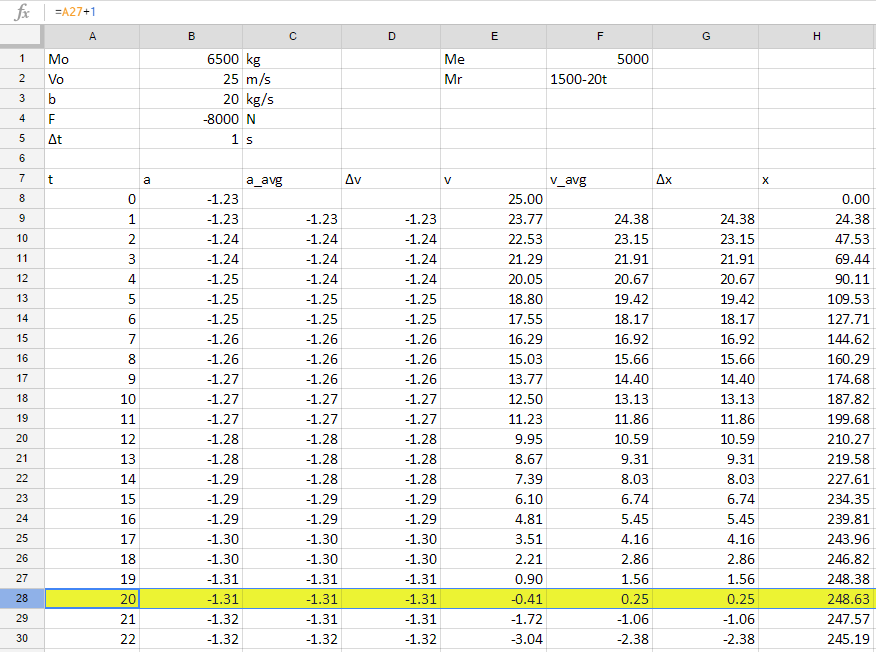
Explanation of Data: Once we had "programmed" Excel according to our lab manual, we received the above data. We use Excel to calculate very small values of time, and then use those small values in the rest of the equations. The smaller we get the time interval to be, the more accurate our answer. We use Excel to approximate the value of our definite integral. This would be helpful in case our integral could not be integrated. We determined our value of position by finding when the velocity would switch from positive to negative. At that point, the elephant would have stopped, and began returning along the same path. We also changed our intervals of time into smaller intervals to see how accurate we could get our answer.

Conclusions:

1. When we found the distance analytically, we got the value x=248.7 meters. When we found the value using Excel, we received the approximate value of x=248.63 meters. These two values only differ by 0.03%! If we were to make the time interval smaller, we would eventually reach approximately the same value as we did analytically.

2. In this particular lab we knew when the time interval was small enough when our values of position were almost exactly the same. If we did not know the value of position as we did it analytically, we could find when velocity was equal to zero, giving us the exact position of the elephant. 

3. In order to calculate this easily, we can plug these numbers into our Excel program. 

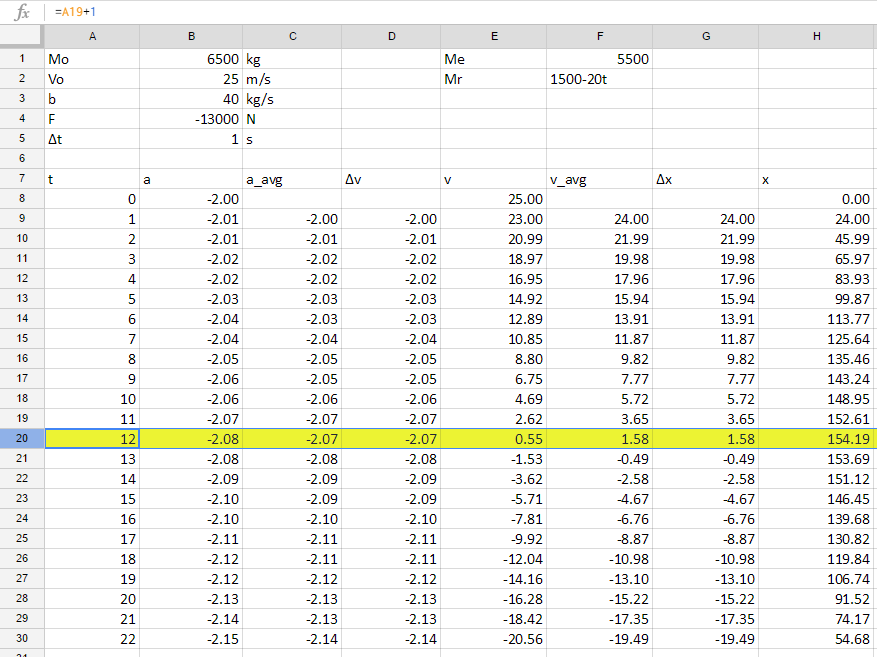
The position is 154.2 meters.

Excel Data for Question 3: